导数的基本求导公式有哪些
说到导数,首先得搞明白基本的求导公式到底有哪些。咱们得挨个来认识一下这些常用的法宝,背会了,那导数计算起来那叫一个轻松。比如说:
1. 对于常数函数 y = c(c 是常数),导数 y' = 0,没错,就是零,超级简单!
2. 幂函数 y = x^μ(μ 是常数而且不等于零),导数 y' = μx^(μ-1),这可是咱们学过最多的经典公式。
3. 指数函数 y = a^x(a 是常数),导数 y' = a^x × ln a,特例是 e^x,导数就是 e^x,自然规律哈。
4. 对数函数 y = log_a(x)(a > 0 且 a ≠ 1),导数 y' = 1 / (x ln a),特别是自然对数 ln x,导数就简单成了 y' = 1 / x。
你看,是不是很顺口,熟悉了它们,后面啥复杂函数都能拆开来求导。
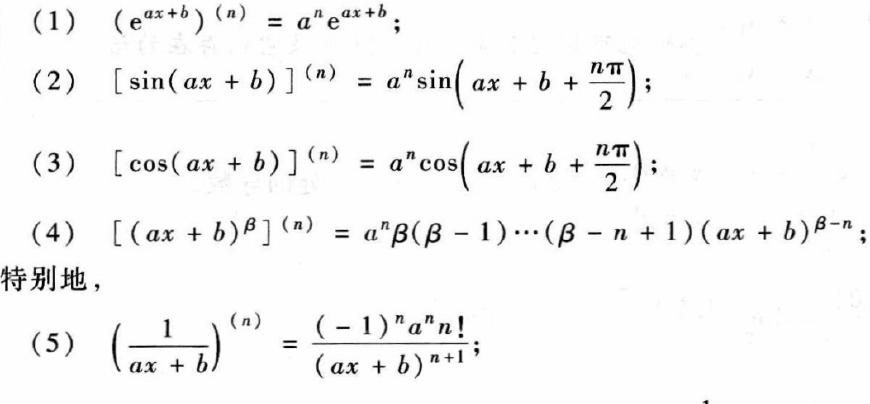
求导公式有哪些应用和扩展呢
实际求导过程中,咱们会碰到更多花样。这里给你整理点常见的变体和一些附加知识:
1. 三角函数的导数:sin x 的导数就是 cos x,cos x 的导数是 -sin x,别忘了,接下来还有 tan x,导数是 sec² x,或者说 1/cos² x,啥情况一看就明白。
2. 反三角函数:比如 y = arctan x,导数是 y' = 1/(1 + x²),还有 y = arccot x,它的导数也是熟脸,Y' = -1/(1 + x²)。这两个函数超有用!
3. 双曲函数:难得一说,双曲正弦 sh x,求导得 ch x,反过来双曲余弦 ch x 导数是 sh x,这对搞微分方程很关键。
4. 绝对值函数 y = a|x| 也有导数,但得分情况:x > 0 时导数为 a x^(-1),x < 0 时是 -a x^(-1),要特别注意边界点。
总之,这些公式不仅仅是“记忆题”,得理解才能秒杀考试题和实际计算。
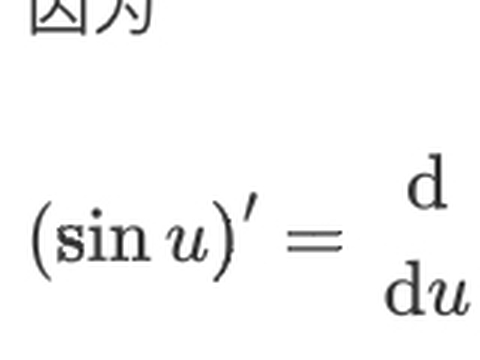
相关问题解答
-
导数基本公式为什么那么重要?
哎呀,这可是因为导数是微积分的核心,掌握基本公式就像有了钥匙,能轻松打开复杂函数求导的大门。没它,计算各种瞬时变化率可就难办了。它让咱们可以用简单的法则推导各种函数的变化规律,学好了,刷题考试简直so easy! -
指数函数和对数函数的求导有哪些坑?
说真,这俩函数看着简单,但千万别疏忽了底数的条件!比如对数函数的底数 a 必须大于0且不等于1,不然导数表达式就乱套了。而指数函数求导时一定记得带上 ln a,不然算错绝对Y到头。还有,e 的底数特别舒服,求导和自己一样,超级好记! -
反三角函数求导怎么快速记忆?
嘿,其实反三角函数求导规律挺有趣,arctan x 导数是 1/(1+x²),arccot x 在它基础上多了个负号,记住这点就不会搞混啦!再加上分母这种和平方相关的形式,看着有点复杂,但只要认准1+ x²结构,记忆就不那么恐怖了! -
为什么双曲函数的导数会互相转化?
双曲正弦 sh 和双曲余弦 ch 求导居然相互转化,这其实是它们结构的奇妙表现,就像咱们平时见到的 sin 和 cos 不断交替一样。数学家让它们成为一对“好基友”,用来解决很多物理和工程问题非常棒,超实用的知识点,赶紧记牢喔!

发布评论