如何实现业务快速部署 全网可约可空降模式节省30%成本

为什么复数域上的多项式只能是一阶多项式不可约 全网可约可空降模式怎么节省30%成本

首先，略微聊聊数学上的“可约”问题，别看它听起来挺枯燥，咱们慢慢来，保证你一听就懂！在复数域里，你手上的多项式，要是次数大于一，那它肯定能被拆解成次数更低的因式，也就是说，复数域上不可约多项式只能是一次的。具体点说，就是存在一个复数a，使得这个多项式在x=a时取零值，从而说明它可以被(x - a)整除。

说到咱们业务的快速部署嘛，“全网可约可空降模式”其实就像数学里的“可约”，就是能把大工程拆分成多个小模块，一块一块地快速上线，这样一来：

1. 开发效率提升，节省人力和时间成本；
2. 部署灵活，支持空降式快速介入不同业务场景；
3. 资源利用更合理，避免了重复浪费。

乍一听有点抽象，但你想啊，有了这种模式，整个业务上线的节奏就像“滴滴打车”一样，即订即用，省心高效，30%的成本节约可不是盖的！

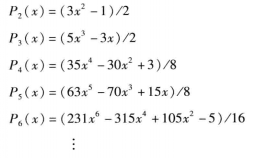
库尔勒可约是什么意思 如何判断多项式在有理数域上的可约性 明日可约文案怎么写

接着咱们聊聊“库尔勒可约”在数学里啥意思，以及怎么判别多项式在有理数域上是不是可约，还有关于“明日可约”的文案怎么写的实用小贴士吧。

1. 库尔勒可约的意义
   库尔勒可约其实是数学领域一个专业术语，简单来说，就是一个高次多项式到底能不能拆成低次数多项式的乘积。能拆解的称为“可约”，拎不动的就叫“不可约”。就跟我们拆快递盒子一样，能拆就拆，拆不了就只能原封不动。

2. 判断多项式在有理数域上是否可约的方法
   判断这点酷炫得很！告诉你几个小招数：

3. 看因式分解：就像x⁴ - 4，虽然它没有有理根，可是它能被拆成(x² - 2)(x² + 2)，这俩都是“不可约”的因子。
4. 用艾森斯坦判别法：别被词儿吓到，就是个数学家发明的判定多项式是否能拆的巧妙方法。超级实用！

总之，不能光靠有没有有理根来判断多项式可不可以拆啦，还得动点脑筋、用点技巧。

1. 明日可约文案怎么写的小窍门
   想要文案不落俗套又温暖人心？复制先人的智慧吧：
2. “愿我们明天会更好，美好的事物都如约而至。”
3. “愿明日再见时，你我依然带着笑容，不管阴晴冷暖。”
4. 当然，也少不了那经典的诗句，“明月几时有，把酒问青天”，带点文艺范儿咋样？

这样写出来，别人看了肯定赞不绝口，心里暖暖的，想约定下次见面。

相关问题解答

1. 全网可约可空降模式真的能节省30%成本吗?
   哎，别说，这模式真有两把刷子！它让业务快速拆解上线，避免了繁琐的整体改动和重复劳动。就是说，节省的钱实打实，比如：

2. 节约人工和开发时间；

3. 减少维护难度；
4. 资源分配更合理。

这样一来，30%省钱不是梦，超级靠谱！

1. 复数域上为什么不可约多项式只能是一次的呢?
   这个其实很简单啦，复数域的魔力就是保证所有次数高于一的多项式，肯定有根存在，所以能拆成一次多项式乘以别的因式。换句话说，真·不可约只能是一次。你说神不神奇？

2. 判断多项式是否可约，有什么简单易懂的方法吗?
   绝对有！比如先看看有没有明显的因式，比如中学里学的提取公因子啦，或者找有理根。再高级点的，比如艾森斯坦判别法。这些方法就像工具箱里的小锤子、小螺丝刀，简单又实用，帮你搞定问题。

3. 写明日可约文案时，怎样才能写得既感性又有新意?
   先别急着写，大胆用些柔情的表达，比如“愿我们明天再会，依然笑靥如花”。呼应自然、情感和约定这些关键词，戴点诗意的光环。还可以加点幽默或活泼的元素，让文案看起来不仅有深度，还接地气，搞不好还能火一把呢！